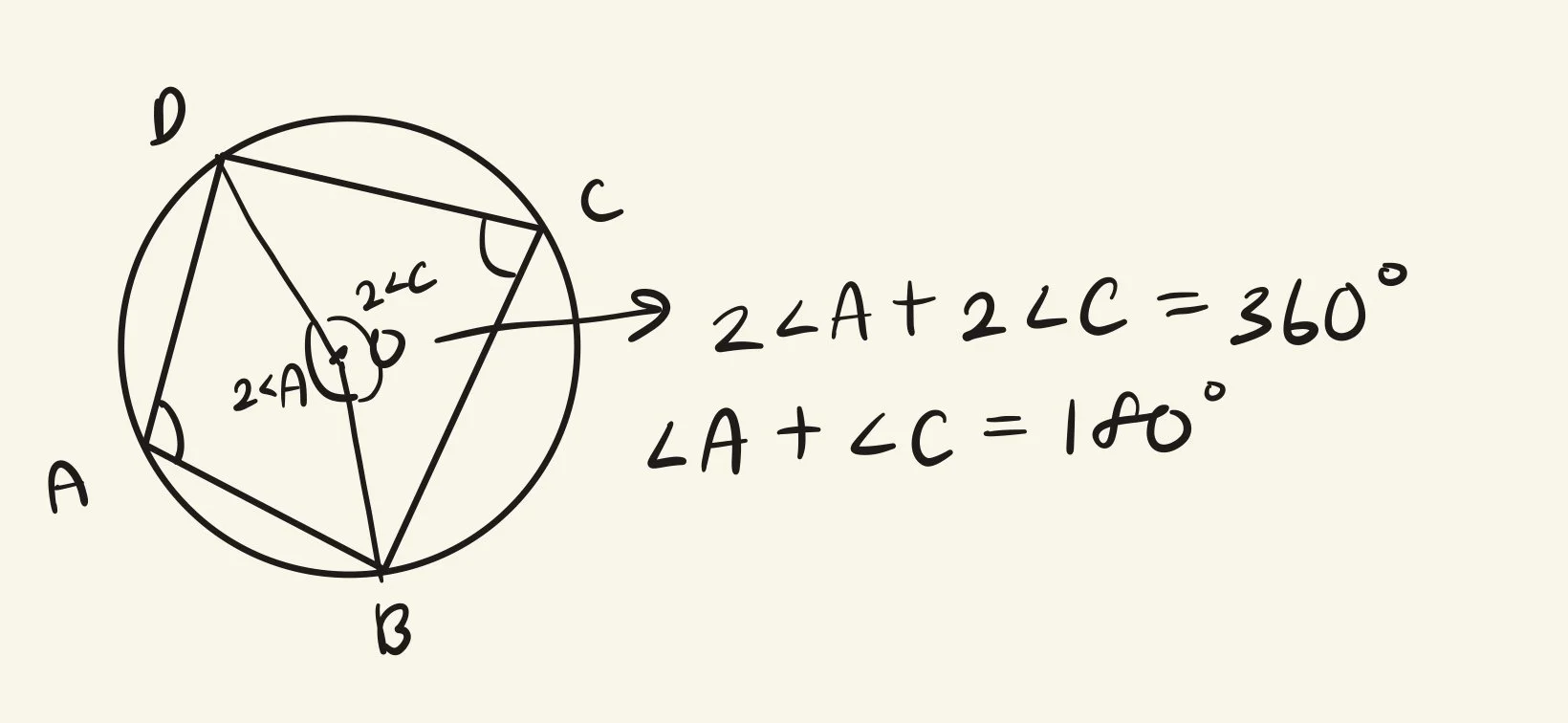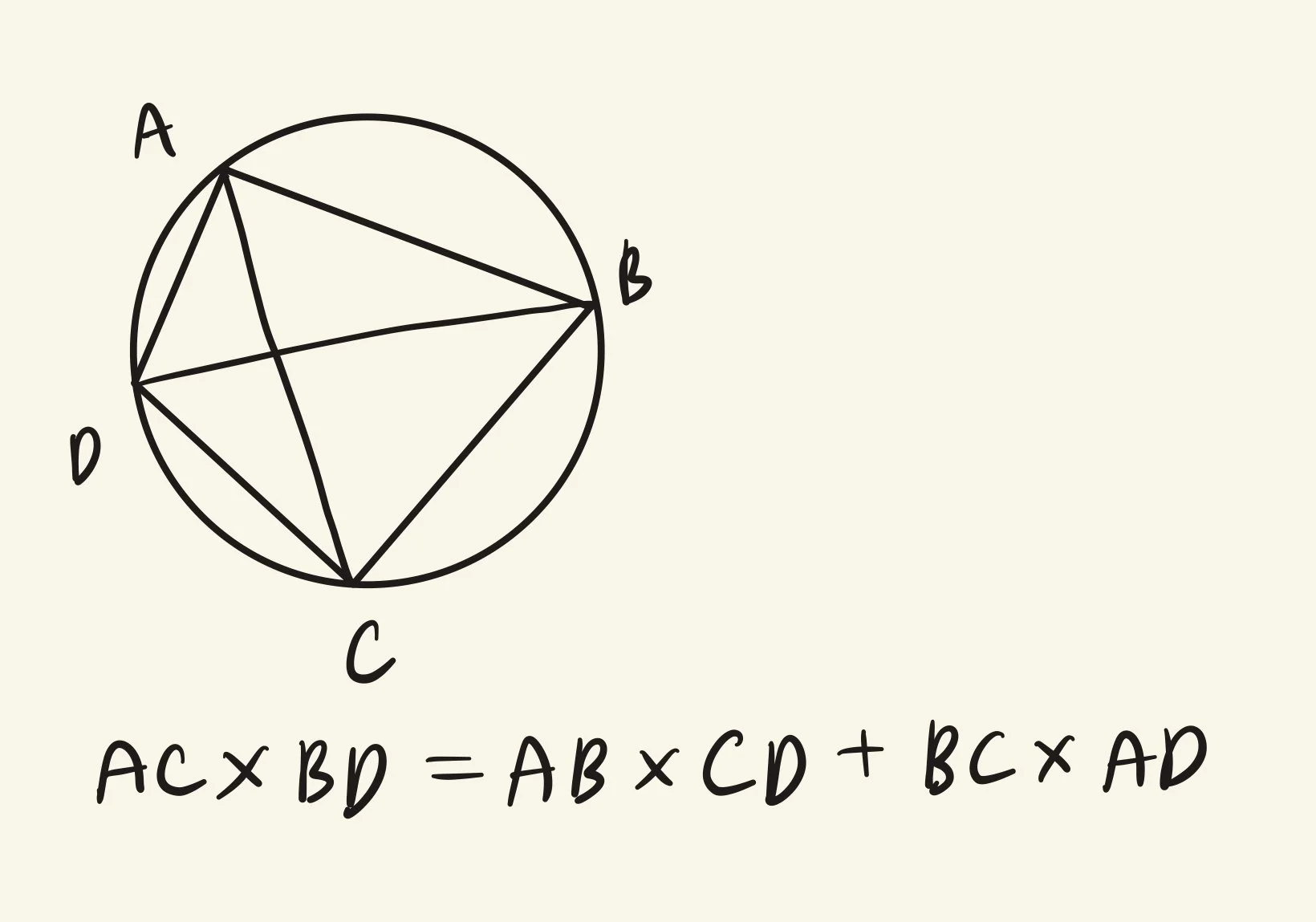Cyclic Quadrilaterals
A cyclic quadrilateral is a quadrilateral that has its four vertices lying on the circumference of a circle. Oftentimes, math problems will utilize this special type of quadrilateral, so it’s important to understand the various properties associated with it.
Property #1: Opposite angles are supplementary
A quadrilateral is cyclic iff (if and only if) ∠A+∠C=180° and∠B+∠D=180°. A rigorous proof of this can be derived from the Inscribed Angle Theorem, which states that an angle at the circumference is half the central angle subtending the same arc. If we drew diagonals, each pair of opposite angles subtends arcs that make up the entire circle (360°), so their halves must sum to 180°, proving they are supplementary.
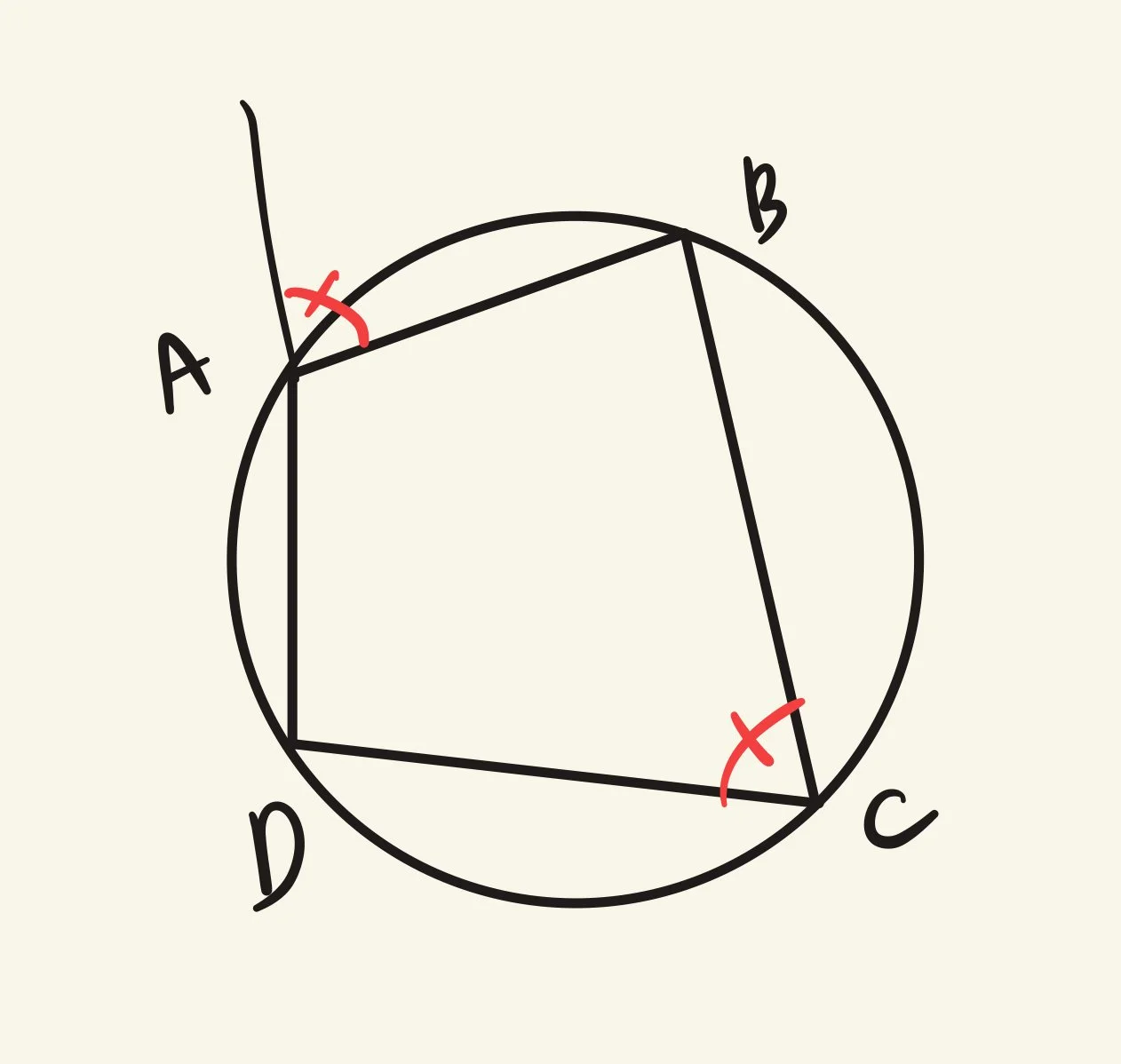
Property #2: Exterior Angle Theorem
In a cyclic quadrilateral, an exterior angle equals the interior opposite angle. The proof for this is easy. Using property #1, opposite angles of a cyclic quad sum to 180 degrees and adjacent angles on a straight line also sum to 180. By setting these two 180-degree equations equal and cancelling the common angle, we show the exterior angle equals the opposite interior angle.
Property #3: Ptolemy’s Theorem
Ptolemy’s theorem is one of the most crucial relationships of cyclic quadrilaterals: the product of the lengths of diagonals equals the sum of the products of the lengths of the opposite sides, expressed as AC * BD = AB * CD + AD * BC. If this relationship is true, we can also prove that the given quadrilateral is cyclic.
Common problem types & solving strategies:
Type 1: Find an Unknown Angle
Strategy:
Look for opposite angles → add to 180°
Check for equal angles from the same arc
Use exterior angle = interior opposite angle if extended
Type 2: Prove a Quadrilateral Is Cyclic
Strategy:
Show a pair of opposite angles sum to 180°, OR
Show an exterior angle equals the opposite interior angle
Type 3: Mixed Triangle & Circle Problems
These problems often involve isosceles triangles, parallel lines, and central vs inscribed angles
Always mark angles you know first, as cyclic relationships usually appear after simplification.