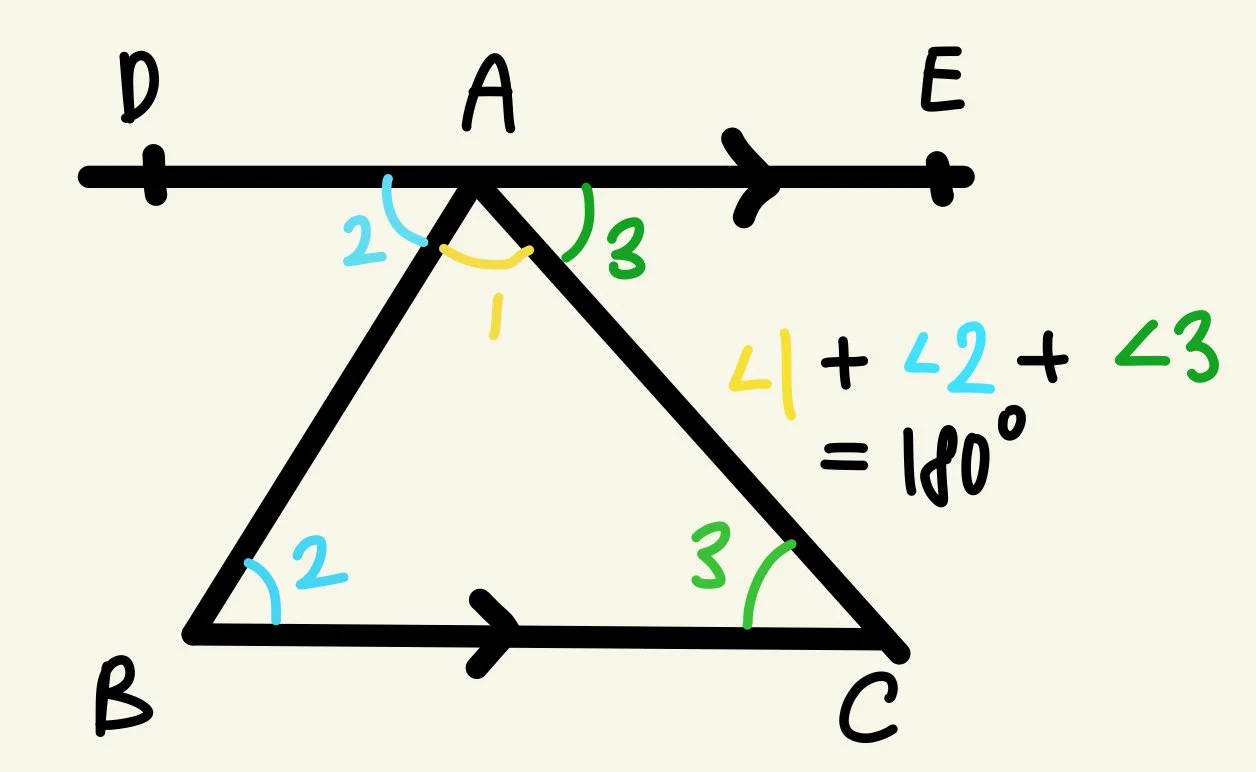ALL TYPES OF ANGLES & WHAT TO DO WITH THEM
There are three types of angles you should know: an acute angle (<90 degrees), an obtuse angle (>90 degrees), and a right angle (=90 degrees).
Outside of the main three, there are also straight angles (= 180 degrees) and reflex angles (>180 but <360 degrees).
New concept: INTERNAL ANGLES
These refer to angles formed by the interior of a polygon (angles inside the shape).
The internal angles of a triangle sum to 180 degrees.
It makes sense that we should generalize the sum of internal angles to an n-sided polygon. The idea is simple: we can divide any polygon into n-2 triangles. Here are a few examples, and you can try for yourself as well.
How do we know the sum of internal angles in a triangle is 180°? There is actually a clever proof for this using straight angles and transversal lines.
I will assume that you understand what a transversal line is, as well as the pairs of angles it creates after intersecting two lines (terms like “alternate interior angles”). If you’re unsure about this, search up “Parallel and transversal lines” on Google!
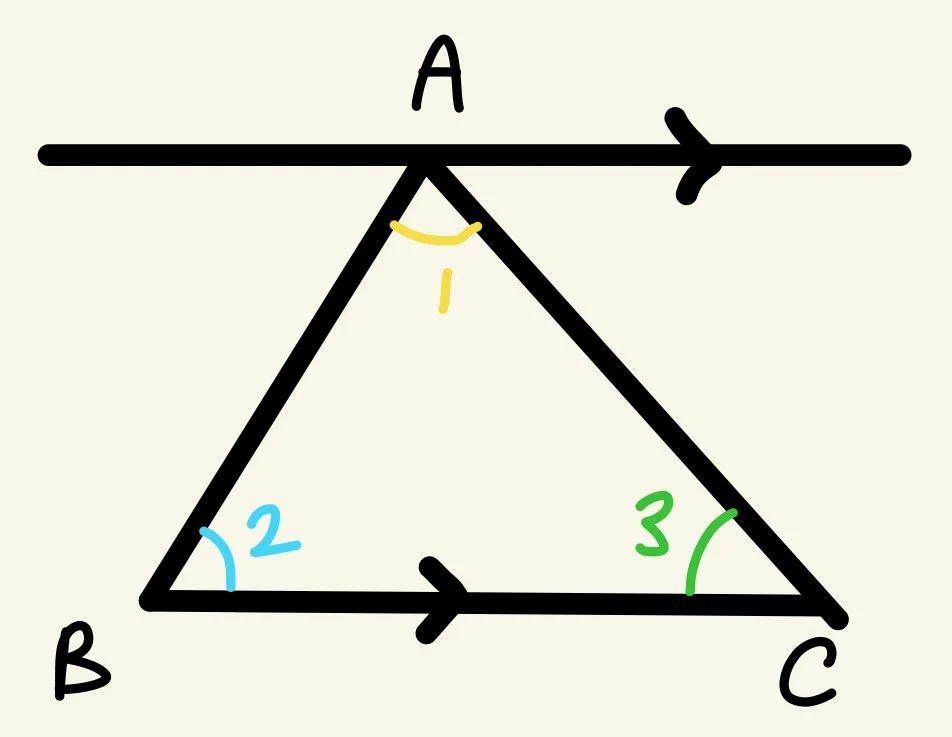
PROOF: Sum of interior angles of a triangle is 180°
Suppose we start with some triangle ABC. Let’s label each of our interior angles as 1, 2, and 3. We can draw a line passing through point A parallel to BC, shown to the left (note the two arrowheads on the lines signal they are parallel).
Now we may view line BA as a transversal intersecting two parallel lines. By the property of transversal lines, ∠BAD = ∠2, and ∠CAE = ∠3.
Quickly, we see that ∠1, ∠2, and ∠3 form a straight angle on line DE. So, ∠1 + ∠2 + ∠3 = 180°, and this completes our proof.